When we say that two particles are quantumly entangled, we mean that the particles cannot be looked at independently even when separated by great distances. This means that if we measure one particle, we will automatically get the measurements of the other.
This concept is spooky, and can be useful in studying the nature of the universe. We can also use this as a form of instant communication. If we take a quantum-entangled photon pair and separate them, altering one would alter the other automatically. Hence we would be able to send information automatically.
To be able to use quantum entangled particles to help us communicate over large distances instantaneously, we would need to first transfer these particles over large distances. The problem with doing so currently is that on the way, sometimes entanglement is lost!
FIG1: Quantum Entanglement of Two Particles: A cartoon depicting the spooky entangled relationship between two particles.

FIG2: Entanglement getting lost: The entanglement of photons can be lost over large distances.
To fix this issue, scientists have proposed the use of quantum repeaters. These are devices which accept an entangled photon, save its entanglement in a cluster of atoms, and then emit another photon which is now the new quantum-entangled photon. In a way, these are kind of like pit-stops for the quantum-entangled photons as they travel.
The way the entanglement of a photon can be saved onto a cluster of atoms is tricky: it can involve the photon mapping its phase (the current point in the wave of a light wave) onto atoms. The phase that is mapped onto the atom is called the geometric phase. This phase is very interesting as it stores information about the previous polarisation states — the different orientations of how the electric field in light vibrates — that the light has been through.
This is very peculiar and amazing! By saying that the light carries geometric phase which saves information about the previous polarisation states the light has been through, we are saying that light knows about its history. For example, when you travel from Wooster to NYC and back, and when you travel from Wooster to Florida and back, you can distinguish both journeys. This is because they were both different paths, although your final start and end points were the same (Wooster). The geometric phase in light shows that even light stores the information needed to distinguish the different previous polarization paths. Additionally, with the geometric phase, we can determine if light has been through a path of polarisation states or not. For example we can distinguish between a person who has travelled from Wooster to NYC and back, and another person who has stayed in Wooster. All this information about the photon’s polarisation path history is given by the geometric phase!
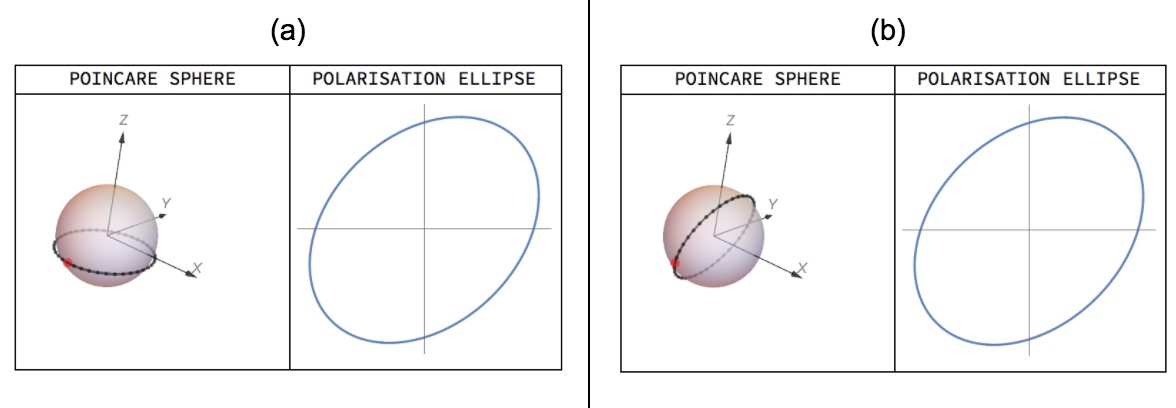
FIG3: Different journeys give different geometrical phases: The red dot represents the starting and ending point of the path (Wooster), and its polarisation state can be seen on the right. The path in figure (a) has a geometrical phase of 8.19 and the path in figure (b) has a geometrical phase of 6.26. These separate paths are analogous to the journies to NYC and Florida from Wooster. The video below shows how different points along the path have different polarisation states (similar to different gas stations along the way to NYC / Florida).

For my Junior Independent Study, I studied how light can retain memory using geometrical phase. A previous Wooster Student, Drew King-Smith, began this study using a model with simple constraints. Working with Dr. Cody Leary, I expanded upon this model by considering factors which would make the model more applicable to our equipment in the laboratory. Through the model we were able to produce predictions for numerous interferograms(interference patterns of light), which tell us about the geometrical phase. These predictions can guide future experimental work in the verification of these interferograms. By doing so we would learn more about the physics of quantum memory!
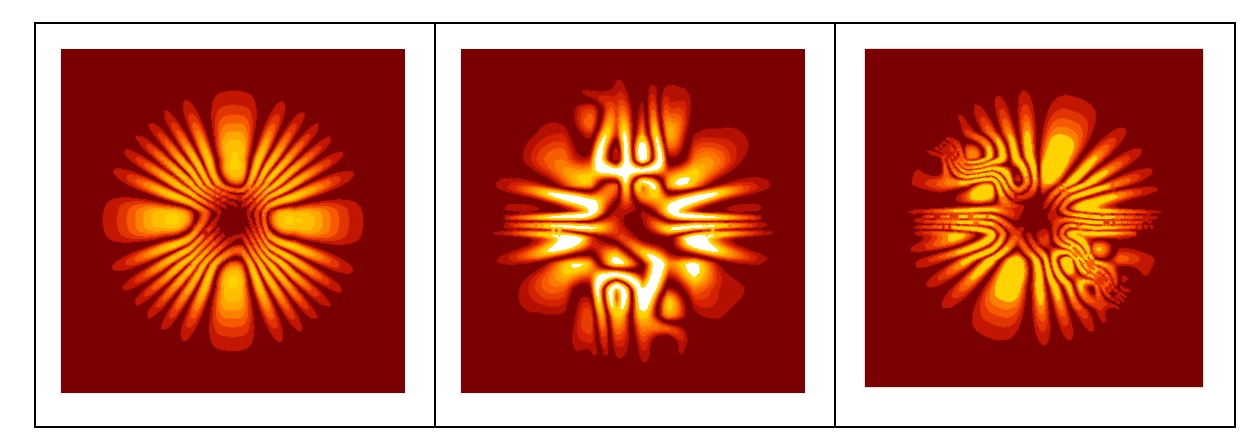
FIG4: Predicted interferograms: These are three interferograms that we predict are created with various parameters.
